Building directional hierarchical structures by stackable molds: brainstorming

Initial ideas for hierarchical structures -- for subsequent work see ClimbingAdhesion

Main.MicheleLanzetta - started 09 Aug 2007

Related work

See also

• StickyBot (one level up)
• MicrohairIntegration -- MarkCutkosky 10 Oct 2005 - 16:52 - r1.8
• HierarchicalFabrication (private)
• HierarchicalTransverse (private)
• LayeredHierarchicalStructures (private)
• MicroAdhesives (private)

Nomenclature (from lab jargon)

Confusion between layer and stack for the hierarchical structure and for the building of parts. In Rapid Prototyping parts are build in layers. So the hierarchy will contain stacks. But in our case we build parts in parallel and then stack (assemble) them, also hierarchical layers sounds better. Issue to be solved by a native American...
Stalk: the larger structure in the hierarchy (cylindrical shape)
Lamella: the larger structures in the hierarchy (triangular or rectangular shape)
Hair: the smallest structure in the hierarchy
Wall: the climbed surface
Toe: the adhesive surface

About hierarchical layers

Layers i-1, i and i+1 displayed

Recommendations (consolidated?)

• structure is expandable to lower and higher size
• size steps can be jumped
• resin i-1, i and i+1 can be different but they needs to be compatible (cure to each other)
• layers can be cast from a positive or they can be any very flat plate (e.g. Si or quartz, but also steel, like in a mesh or filter) with holes
• each layer can be extruded and then stacked
• the packing of stalks should achieve the maximum density

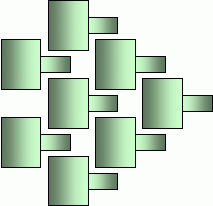Only a small area of the base surface is lost

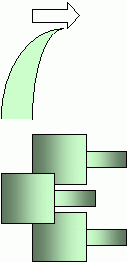Bending the lamella by applying a shear load to the mould in order to achieve an even higher packing

Some open problems

• serial or parallel process = build each layer separately and then joint or cast?
• shape of each hair? (see directional structures)
• size ratio between layers?
• same resin to cast at the same time or cast individual layers and then cure?

Directional adhesion (about the shape of stalks)

What optimal stalk shape produces directional adhesion? Optimal means:

• enough adhesion,
• directional,
• easy to (mass) produce

How to make the toe directional:

• by having stalks that offer the maximum possible surface when exposed to the favorable direction and inversely offering the minimum surface when exposed in the reverse direction

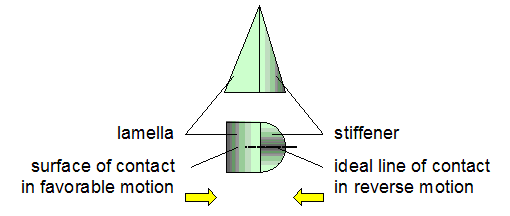
• stalks need to be slender enough to provide sufficient bending and surface exposition

Example of a (tri-directional) surface, based on a simple geometry. At its turn, each of the three vertical edges acts like a stiffener for the opposite surface.

Please also see the first two figures of this page with additional stalk shapes.

Stalk distribution

Please also see the figures above. How to make the toe omni directional or with n preferential adhesion directions:

• by orienting each stalk in a random direction
• or orienting each of the n fractions of the stalks in a preferential direction (by a random or by a systematic orientation distribution)

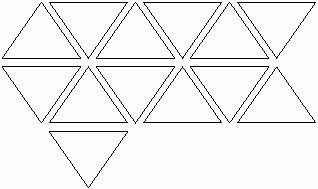Example of tri-directional surface. Only one third of the stalks are active in each of the three preferential directions. Multi-directional surfaces are useful for the robot for squeezing.

Dimensioning the stalks

Dimensional constraints

• the bending force, given by the length and the section of the stalk and its Young%u2019s module must equal the surface energy for adhesion to the surface material [Soto]
• the stiffener force should be lower than bending force to allow the bending (but the stiffener is made with the same material and has a smaller section anyway) but high enough to prevent clumping among stalks by pushing them back to the straight position
• the number of layers depends on the height and distribution of asperities of the wall surface

Attaching hair to stalks

Tilted haired lamella

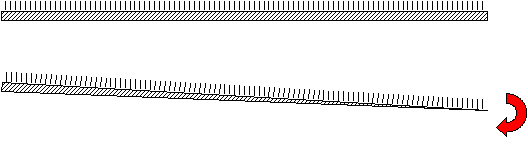Two-level hierarchical structure obtained by tilting the mould.

Tilted Matrix of pins

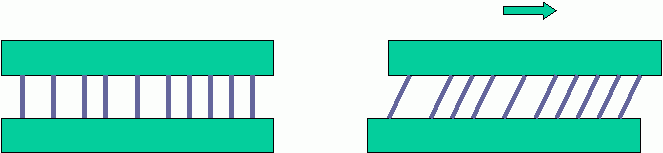A positive of stalks to create a mold on top of a hair stack, can be made using a matrix of pins threaded into two parallel plates, which can be slid to achieve the required angle.

New approach! (private)

Please visit HierarchicalTransverse? (private)