new web: http://bdml.stanford.edu/pmwiki
TWiki > Rise Web>ClimbingRobot > RobotAnalysis > CbotStaticModeling>ConvexShear (04 Apr 2007, MarkCutkosky)
Rise Web>ClimbingRobot > RobotAnalysis > CbotStaticModeling>ConvexShear (04 Apr 2007, MarkCutkosky)
It appears that a coef. of friction of 2 is about the best we can get in short term. See bottom of page for how this affects things... -mrc June 1 2004
Convex (or concave) surface analysis
Suppose the robot is climbing on a smooth, gently curved surface. We are looking down at the front of the robot and we see two front limbs in contact with the wall. Suppose we have a materials on the feet that provide little or no adhesion, but a large effective coefficient of friction.The question is: If we apply lateral forces, how much net pull into the wall can we sustain by virtue of the convexity of the surface?
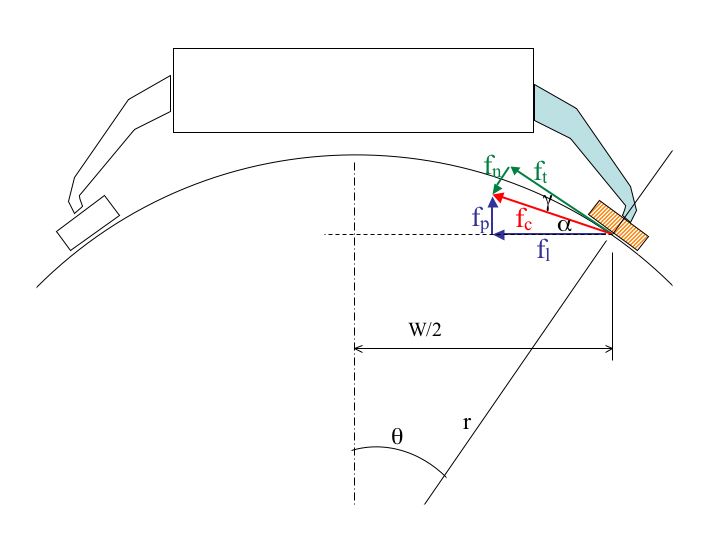 Nomenclature:
Nomenclature: -
 = the width of the robot
= the width of the robot
-
 = radius of curvature of the convex surface
= radius of curvature of the convex surface
-
 = half of the angle spanned by the robot
= half of the angle spanned by the robot
-
 = net pull-in force that helps prevent pitchback
= net pull-in force that helps prevent pitchback
-
 = lateral (internal or "pinch") force applied by robot legs
= lateral (internal or "pinch") force applied by robot legs
-
 = normal force at the contact
= normal force at the contact
-
 = tangential force at the contact
= tangential force at the contact
-

-

-

- if on the verge of slipping, then
 , where
, where  = coefficient of friction
= coefficient of friction
-

 , and
, and  . Then
. Then  and
and  Some example numbers letting w=1 (stance = unit width) and radius of curvature as multiples of w:
Some example numbers letting w=1 (stance = unit width) and radius of curvature as multiples of w:
w r theta mu gamma alpha fl fp 1.000 1.000 0.524 5 0.197 0.326 5 1.691 1.000 1.500 0.340 5 0.197 0.142 5 0.717 1.000 2.000 0.253 5 0.197 0.055 5 0.277 1.000 4.000 0.125 10 0.100 0.026 5 0.128 1.000 6.000 0.083 15 0.067 0.017 5 0.084 1.000 8.000 0.063 20 0.050 0.013 5 0.063 1.000 1.000 0.524 2 0.464 0.060 5 0.300-- MarkCutkosky - 12 May 2004
Ideas, requests, problems regarding TWiki? Send feedback