new web: http://bdml.stanford.edu/pmwiki
TWiki > Rise Web>ClimbingRobot > RobotAnalysis>CbotStaticModeling (14 Jun 2005, MarkCutkosky)
Rise Web>ClimbingRobot > RobotAnalysis>CbotStaticModeling (14 Jun 2005, MarkCutkosky)
-- MarkCutkosky - 12 Aug 2003 added some links and anchor to Cbot Files in this document.
(Newest stuff is at the bottom of this page). -- DanielSantos? - 17 Jun 2003 Started. This page is devoted to some static modeling of a climbing robot. Initially, this will be sketching up some simple robot concepts (e.g. 1 rigid body and 2 legs (fore and hind), and using Matlab to analyze effects of leg placement, center of gravity, etc.. Also, non-Coulomb friction models (e.g. a friction + adhesion model) will be explored for the leg contacts and will eventually be incorporated into the static models. Matlab files and functions to allow analysis of various types of robot configurations will be written. e.g. How much adhesion force is required at the foreleg as a function of the position of the center of gravity.?
-- MarkCutkosky - 02 Jul 2003 A couple of notes about where this is headed: We are looking initially at some simple quasi-static modeling of a climbing robot to get insight about foot placement and force distribution. For a first pass, Daniel is following a method adapted from the grasp analysis paper by Kerr and Roth (IJRR Vol. 4, No. 4, 1986 -- see list of links below) which treats grasp formulation as a linear programming problem. Of course, the contact and friction constraints are somewhat different, but this was, in my opinion, the first and simplest "good" treatment of grasping and it is easily adapted to climbing. Later inertial forces can be added using a d'Alembert formulation. We're assuming t hat coriolis, etc. terms will be negligible. Another useful paper is Bretl et al. (see list below). In parallel, JonathanClark and AMcClung are looking at LegDesign and DynamicModeling.
A few links:
-- DanielSantos? - 29 Jul 2003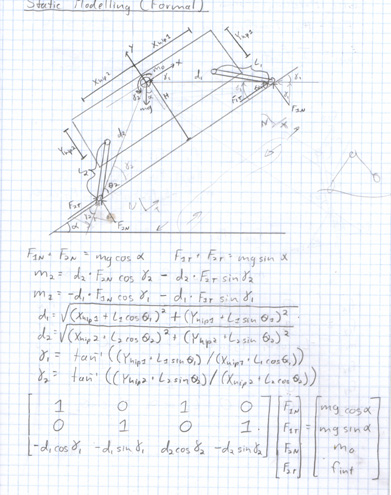 Initial (planar) static model is complete. This model uses 3 external equilibrium equations (Net Force in Tangential and Normal must sum to zero and Net Moment about the Center of Gravity must sum to zero) and a set of inequality constraints (currently based on a Coulomb Friction Model) to solve for 4 contact forces (Front/Rear Normal/Tangential). The null space of the equilibrium equations contains relationships between the contact forces and Internal Body Forces. The Internal Body Forces are chosen such that the inequality constraints are furthest from being violated (See above scanned notes from Kerr and Roth for more details). Also, below is a PowerPoint Presentation that goes into more detail on the solution that was implemented and also discusses some of the initial findings that the solution has given.
The solution has been implemented in Matlab using its GUI capabilities. Bringing up the GUI window provides an interface to modify the geometric parameters of the Cbot and then analyze the contact forces at the front and rear foot as a function of the angle of inclination (0-90 degrees). The interface also allows application of an external thrust vector to the Cbot (see PartridgeThrust). The four required Matlab files to run the analysis are below. Cbot_config.m is a file with the geometric parameters describing the CBot. Cbot.fig is a Matlab figure file for the GUI. Cbot.m is a Matlab 'm' file for the GUI. Cbot_Analysis.m performs the actual analysis.
Note: These files were updated on 14 Aug 2003. Please see below for explanation of changes made.
Initial (planar) static model is complete. This model uses 3 external equilibrium equations (Net Force in Tangential and Normal must sum to zero and Net Moment about the Center of Gravity must sum to zero) and a set of inequality constraints (currently based on a Coulomb Friction Model) to solve for 4 contact forces (Front/Rear Normal/Tangential). The null space of the equilibrium equations contains relationships between the contact forces and Internal Body Forces. The Internal Body Forces are chosen such that the inequality constraints are furthest from being violated (See above scanned notes from Kerr and Roth for more details). Also, below is a PowerPoint Presentation that goes into more detail on the solution that was implemented and also discusses some of the initial findings that the solution has given.
The solution has been implemented in Matlab using its GUI capabilities. Bringing up the GUI window provides an interface to modify the geometric parameters of the Cbot and then analyze the contact forces at the front and rear foot as a function of the angle of inclination (0-90 degrees). The interface also allows application of an external thrust vector to the Cbot (see PartridgeThrust). The four required Matlab files to run the analysis are below. Cbot_config.m is a file with the geometric parameters describing the CBot. Cbot.fig is a Matlab figure file for the GUI. Cbot.m is a Matlab 'm' file for the GUI. Cbot_Analysis.m performs the actual analysis.
Note: These files were updated on 14 Aug 2003. Please see below for explanation of changes made.
8-13-03 MarkCutkosky
Next steps
-- DanielSantos? - 14 Aug 2003 Two changes were made to the files below from the previous release. First, a bug was fixed having to do with the use of atan vs. atan2. This bug was related to the application of the external thrust vector. Second, a new feature has been added to the GUI. The GUI now has the ability to save and load Cbot configurations. Simply type a descriptive name in the Save File text box and push on Save File.
-- DanielSantos? - 25 Aug 2003 Model has been extended to quasi-3D. By specifying a width for the robot, the front leg is moved to the left of the CG and the rear leg is moved to the right of the CG, but legs are still parallel to the sagittal plane. Also, the model now allows for arbitrary foot contact orientations, also in the sagittal plane. This allows analysis of the robot on concave or convex surfaces w.r.t the direction of motion, but not concave or convex surfaces in the lateral direction (e.g. an animal climbing up a tree). The graphical interface has also been altered. Along with all the previous information, the interface now shows the feasible range of the internal body force. The tangential forces in the X and Y directions are still solved for using the optimal choice of internal body force, which is also shown. A schematic representation of the foot contacts has been added to disply which of the friction constraints are active at a particular angle. For each foot there are 4 friction constraints resulting from "|Fx|+|Fy|<=u*Fz". A plot of the lateral foot contact forces has also been added.
-- DanielSantos? - 4 Sep 2003 Interface has now been given the ability to specify how the contact forces are solved. Previous version solved for contact forces using the "optimal" internal body force within the feasible range of internal body forces. The "optimal" body force was the internal body force that was farthest away from violating any of the friction constraints. Now, the user can specify at what percentage of the range between the lower and upper limits of the internal body force the contact forces should be solved, i.e. the "optimal" solution corresponds to 50%, equidistant from the lower and upper bounds. Minor updates to graphical interface have been made. Model schematic is now drawn in 3D and can be rotated by clicking and dragging anywhere in the plot of the model schematic. Model schematic is also now shown at an angle of inclination specified by the user. Instructions: Download the Cbot zip file and extract all the files into a directory of your choosing. Open Matlab. Change the current working directory to the directory where you extracted all the files. Type 'Cbot' at the command prompt. MarkCutkosky 05-12-04
Suppose we have very little adhesion to work with, but a large effective coefficient of friction. See ConvexShear for a back-of-envelope calculation of how much benefit can we get from climbing on a curved surface (convex or concave)
(Newest stuff is at the bottom of this page). -- DanielSantos? - 17 Jun 2003 Started. This page is devoted to some static modeling of a climbing robot. Initially, this will be sketching up some simple robot concepts (e.g. 1 rigid body and 2 legs (fore and hind), and using Matlab to analyze effects of leg placement, center of gravity, etc.. Also, non-Coulomb friction models (e.g. a friction + adhesion model) will be explored for the leg contacts and will eventually be incorporated into the static models. Matlab files and functions to allow analysis of various types of robot configurations will be written. e.g. How much adhesion force is required at the foreleg as a function of the position of the center of gravity.?
-- MarkCutkosky - 02 Jul 2003 A couple of notes about where this is headed: We are looking initially at some simple quasi-static modeling of a climbing robot to get insight about foot placement and force distribution. For a first pass, Daniel is following a method adapted from the grasp analysis paper by Kerr and Roth (IJRR Vol. 4, No. 4, 1986 -- see list of links below) which treats grasp formulation as a linear programming problem. Of course, the contact and friction constraints are somewhat different, but this was, in my opinion, the first and simplest "good" treatment of grasping and it is easily adapted to climbing. Later inertial forces can be added using a d'Alembert formulation. We're assuming t hat coriolis, etc. terms will be negligible. Another useful paper is Bretl et al. (see list below). In parallel, JonathanClark and AMcClung are looking at LegDesign and DynamicModeling.
A few links:
- some notes and relevant scanned pages from Kerr and Roth
- A good paper by Bretl, Rock & Latombe on a human-inspired climbing robot planner
-- DanielSantos? - 29 Jul 2003
 Initial (planar) static model is complete. This model uses 3 external equilibrium equations (Net Force in Tangential and Normal must sum to zero and Net Moment about the Center of Gravity must sum to zero) and a set of inequality constraints (currently based on a Coulomb Friction Model) to solve for 4 contact forces (Front/Rear Normal/Tangential). The null space of the equilibrium equations contains relationships between the contact forces and Internal Body Forces. The Internal Body Forces are chosen such that the inequality constraints are furthest from being violated (See above scanned notes from Kerr and Roth for more details). Also, below is a PowerPoint Presentation that goes into more detail on the solution that was implemented and also discusses some of the initial findings that the solution has given.
The solution has been implemented in Matlab using its GUI capabilities. Bringing up the GUI window provides an interface to modify the geometric parameters of the Cbot and then analyze the contact forces at the front and rear foot as a function of the angle of inclination (0-90 degrees). The interface also allows application of an external thrust vector to the Cbot (see PartridgeThrust). The four required Matlab files to run the analysis are below. Cbot_config.m is a file with the geometric parameters describing the CBot. Cbot.fig is a Matlab figure file for the GUI. Cbot.m is a Matlab 'm' file for the GUI. Cbot_Analysis.m performs the actual analysis.
Note: These files were updated on 14 Aug 2003. Please see below for explanation of changes made.
Initial (planar) static model is complete. This model uses 3 external equilibrium equations (Net Force in Tangential and Normal must sum to zero and Net Moment about the Center of Gravity must sum to zero) and a set of inequality constraints (currently based on a Coulomb Friction Model) to solve for 4 contact forces (Front/Rear Normal/Tangential). The null space of the equilibrium equations contains relationships between the contact forces and Internal Body Forces. The Internal Body Forces are chosen such that the inequality constraints are furthest from being violated (See above scanned notes from Kerr and Roth for more details). Also, below is a PowerPoint Presentation that goes into more detail on the solution that was implemented and also discusses some of the initial findings that the solution has given.
The solution has been implemented in Matlab using its GUI capabilities. Bringing up the GUI window provides an interface to modify the geometric parameters of the Cbot and then analyze the contact forces at the front and rear foot as a function of the angle of inclination (0-90 degrees). The interface also allows application of an external thrust vector to the Cbot (see PartridgeThrust). The four required Matlab files to run the analysis are below. Cbot_config.m is a file with the geometric parameters describing the CBot. Cbot.fig is a Matlab figure file for the GUI. Cbot.m is a Matlab 'm' file for the GUI. Cbot_Analysis.m performs the actual analysis.
Note: These files were updated on 14 Aug 2003. Please see below for explanation of changes made.
8-13-03 MarkCutkosky
Next steps
- allow for arbitrary foot contact orientations (e.g. curved surfaces).
- extend to quasi-3D (front/rear limb in different vertical planes)
- include some inertial forces and moments (pseudo dynamic)
- experiment with different friction/adhesion models
-- DanielSantos? - 14 Aug 2003 Two changes were made to the files below from the previous release. First, a bug was fixed having to do with the use of atan vs. atan2. This bug was related to the application of the external thrust vector. Second, a new feature has been added to the GUI. The GUI now has the ability to save and load Cbot configurations. Simply type a descriptive name in the Save File text box and push on Save File.
-- DanielSantos? - 25 Aug 2003 Model has been extended to quasi-3D. By specifying a width for the robot, the front leg is moved to the left of the CG and the rear leg is moved to the right of the CG, but legs are still parallel to the sagittal plane. Also, the model now allows for arbitrary foot contact orientations, also in the sagittal plane. This allows analysis of the robot on concave or convex surfaces w.r.t the direction of motion, but not concave or convex surfaces in the lateral direction (e.g. an animal climbing up a tree). The graphical interface has also been altered. Along with all the previous information, the interface now shows the feasible range of the internal body force. The tangential forces in the X and Y directions are still solved for using the optimal choice of internal body force, which is also shown. A schematic representation of the foot contacts has been added to disply which of the friction constraints are active at a particular angle. For each foot there are 4 friction constraints resulting from "|Fx|+|Fy|<=u*Fz". A plot of the lateral foot contact forces has also been added.
-- DanielSantos? - 4 Sep 2003 Interface has now been given the ability to specify how the contact forces are solved. Previous version solved for contact forces using the "optimal" internal body force within the feasible range of internal body forces. The "optimal" body force was the internal body force that was farthest away from violating any of the friction constraints. Now, the user can specify at what percentage of the range between the lower and upper limits of the internal body force the contact forces should be solved, i.e. the "optimal" solution corresponds to 50%, equidistant from the lower and upper bounds. Minor updates to graphical interface have been made. Model schematic is now drawn in 3D and can be rotated by clicking and dragging anywhere in the plot of the model schematic. Model schematic is also now shown at an angle of inclination specified by the user. Instructions: Download the Cbot zip file and extract all the files into a directory of your choosing. Open Matlab. Change the current working directory to the directory where you extracted all the files. Type 'Cbot' at the command prompt. MarkCutkosky 05-12-04
Suppose we have very little adhesion to work with, but a large effective coefficient of friction. See ConvexShear for a back-of-envelope calculation of how much benefit can we get from climbing on a curved surface (convex or concave)
Ideas, requests, problems regarding TWiki? Send feedback