new web: http://bdml.stanford.edu/pmwiki
TWiki > Rise Web>ClimbingRobot > ClimbingConcepts > SpinedSurfaces > SurfaceProfileAcquisition>SurfaceProfileSimulation (10 Jan 2005, MarkCutkosky)
Rise Web>ClimbingRobot > ClimbingConcepts > SpinedSurfaces > SurfaceProfileAcquisition>SurfaceProfileSimulation (10 Jan 2005, MarkCutkosky)
This page talks about the results of Alan's matlab simulations with Michele's surface profiles.
-- AlanAsbeck - 10 Nov 2004
MarkCutkosky Jan 10 2005 - the spine/surface interaction computation is somewhat similar to the computation of swept volumes of end mills for CNC toolpath planning. There is a lot of literature on this. One of the benchmark papers is: Wang, W.P., and Wang,K.K., 1986, “Geometric Modeling for Swept Volume of Moving Solids”, IEEE Computer Graphic Applications, Vol 6:12, pp. 8-17. http://www.sdpsnet.org/journals/vol4-1/cutter.pdf Wang, and Anderson (at Purdue), Elaine Cohen (Utah) are among those who are written in this area. Also Allison Okamura's PhD thesis has some related stuff on "traced surfaces" and what they are. (http://www-cdr.stanford.edu/touch/publications/okamura_thesis.pdf)
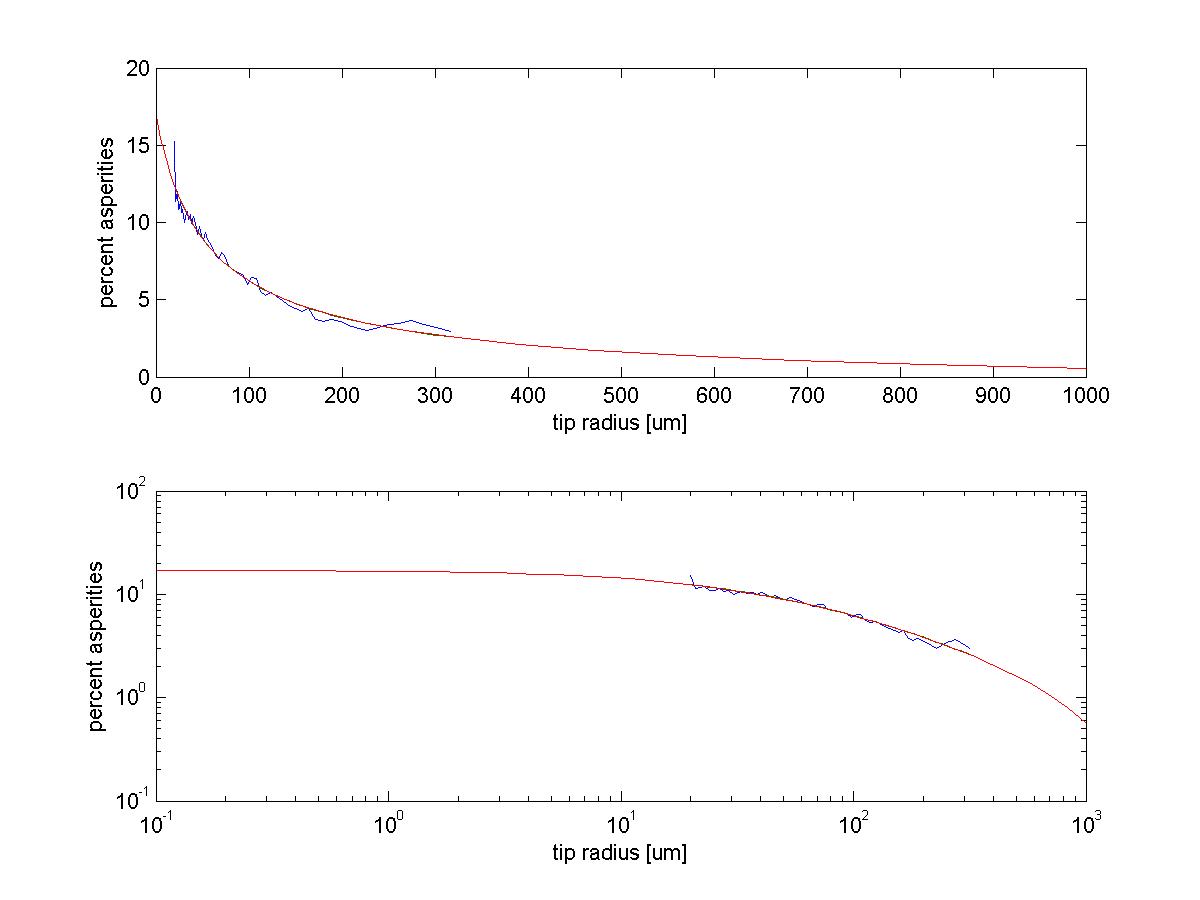
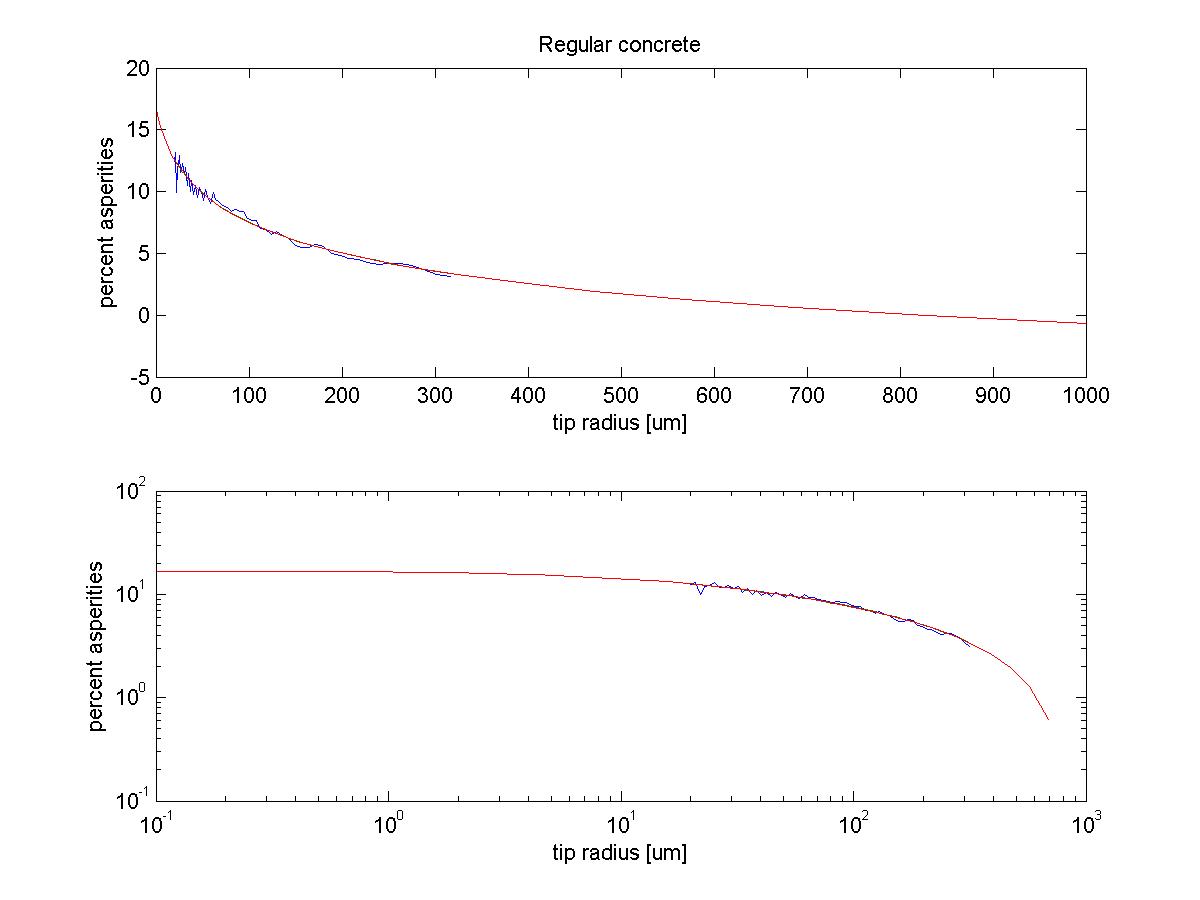
I fitted a function of the form: % = C*(r-B)^(-A) + D where % = linear percent asperity coverage, r = spine tip radius. With two types of concrete, the following parameters were generated:
MarkCutkosky Jan 10 2005 - the spine/surface interaction computation is somewhat similar to the computation of swept volumes of end mills for CNC toolpath planning. There is a lot of literature on this. One of the benchmark papers is: Wang, W.P., and Wang,K.K., 1986, “Geometric Modeling for Swept Volume of Moving Solids”, IEEE Computer Graphic Applications, Vol 6:12, pp. 8-17. http://www.sdpsnet.org/journals/vol4-1/cutter.pdf Wang, and Anderson (at Purdue), Elaine Cohen (Utah) are among those who are written in this area. Also Allison Okamura's PhD thesis has some related stuff on "traced surfaces" and what they are. (http://www-cdr.stanford.edu/touch/publications/okamura_thesis.pdf)
I fitted a function of the form: % = C*(r-B)^(-A) + D where % = linear percent asperity coverage, r = spine tip radius. With two types of concrete, the following parameters were generated:
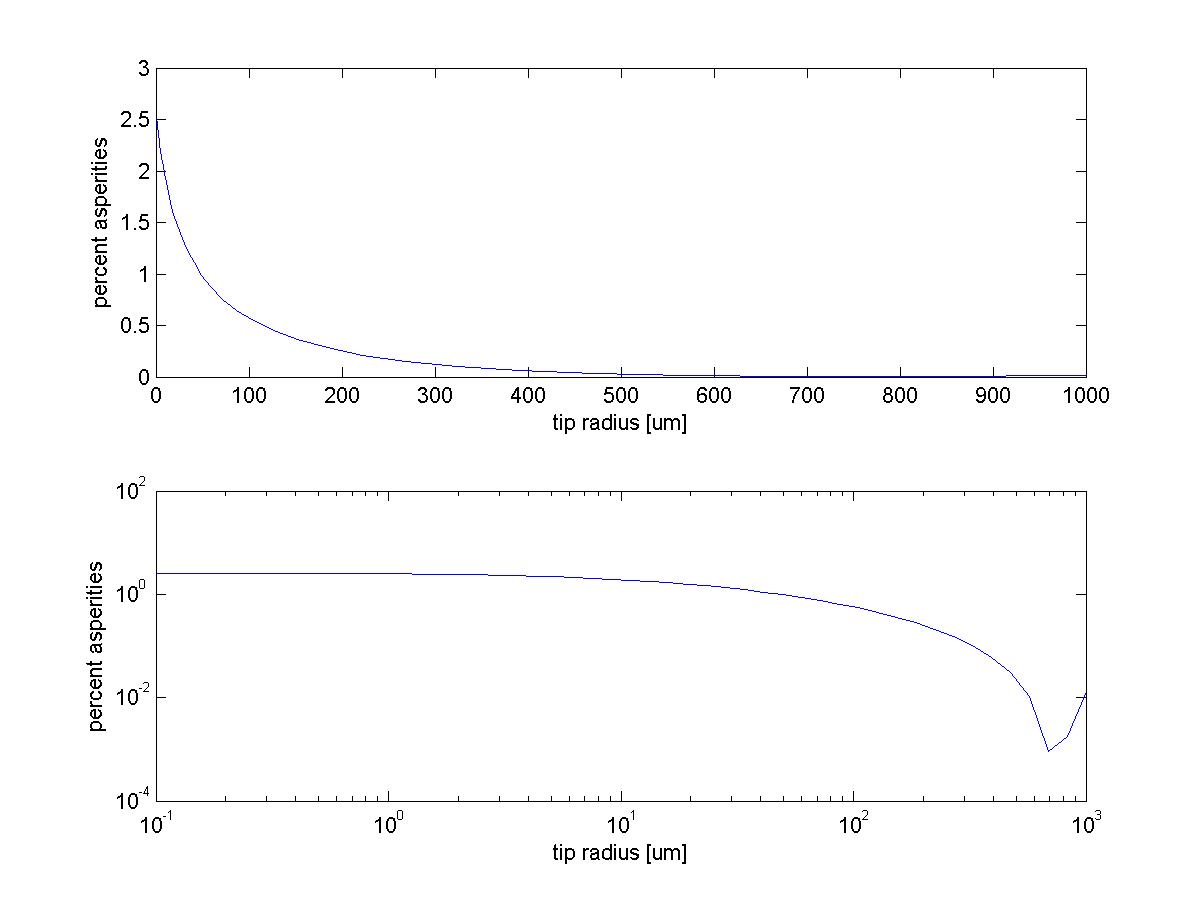
regular concrete: bestcoeffs = [A B C D] = [ 0.0238895 -15.1211 1.922 -1.64045 ] error = 0.001446 lapis concrete: bestcoeffs = [A B C D] = [ 0.7116 -39.4381 2.49014 -0.0121226 ] error = 0.001745Pictures of both of these are below. I think the lapis function is a little better-looking than the one for regular concrete. Note that they both have approximately the same percentage of asperities for r=0, which is nice. So, if you want to square this to get area, you should do: %area = ( C*(r-B)^(-A) + D) )^2 or with the numbers for the lapis concrete, %area = ( 2.49*(r + 39.44)^(-0.7116) - 0.01212 )^2 A picture of this is below also. If you instead want to multiply this by 0.95, do (for the lapis concrete): %area = 0.95 * ( 2.49*(r + 39.44)^(-0.7116) - 0.01212 ) A few comments: with SpinyBot II, the tip radius was about 10-25um (from Michele's measurements.. see ClawTipMeasures). This puts the linear percentage above 10%, and it doesn't get too much higher as the tip radius gets to 0. I think practically the curve goes up a little faster because the physical mechanism by which spine tips engage the surface is somewhat different than the mechanism I assumed in the simulation--the little tips can cover probably about 30-40% of the surface I think. But, in either case, the amount that can be gained by having smaller spines does not seem to be a huge amount.. maybe at best twice the percentage of what it is now.
- Lapis Concrete:
- Regular Concrete:
- Linear percentage squared, Lapis Concrete:
Ideas, requests, problems regarding TWiki? Send feedback