Spine/Asperity Contact Models

(for SpinyBot and RisePlatform with microspines)

• Introduction
• Spine plastic failure in bending
• Spine unbending
• Asperity failure

---

Introduction

We have observed that spine/asperity contacts tend to fail in one of three ways:

• the spine fails plastically at its base due to tensile stress from bending
• the deflects elastically such that it slips off the asperity
• the asperity fails

This page presents our models to describe each of these failure modes and compares them with results of experiments.

Spine plastic failure in bending

Spine unbending

One possible mode of adhesion failure between an asperity and the small curved spines occurs when there is gross deflection of the spine. The most likely mode for this failure would occur due to tip rotation. Here we apply Castigilano's 2nd Thm to solve for spine tip deflections and rotations

The basic approach is to (1) formulate the energy stored in the beam.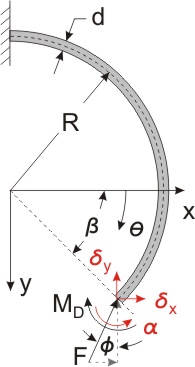

And then (2) take the partial derivative with respect to the force corresponding to the displacement we are trying to solve for.

In the case of the tip rotation, a "dummy moment" is applied at the tip and then set to zero after the partial derivative has been taken.

The following enclosure derives the tip deflection and rotation of a spine based on Castigilano's 2nd Thm. The spine is modelled as a curved beam of constant, circular cross-section.

• Derivation of tip deflection & rotation for curved beam and associated curved beam mathematics file.

Note that these particular equations only hold when the radius of curvature of the curved beam is in excess of 10x it's thickness (valid for our spines).

Asperity failure

It's not clear what the best model is for spines in contact with "cementitious" materails like concrete. There is some literature on erosion and localized failure models for such materials. Momber (2004 - see citation below) investigates erosion of concrete and rock blasted by small particles. The failure analysis starts with Hertzian contact stresses and considers the fracture toughness of the material. (See page 72).

Damage to Rocks and Cementitious Materials from Solid Impact
Journal   Rock Mechanics and Rock Engineering
Publisher   Springer Wien
ISSN   0723-2632 (Print) 1434-453X (Online)
Subject   Engineering and Earth and Environmental Science
Issue   Volume 37, Number 1 / February, 2004
DOI   10.1007/s00603-003-0012-1
Pages   57-82
SpringerLink Date   Thursday, February 19, 2004

---

12-13-04 MarkCutkosky: New stuff after reading K.L. Johnson and Sheldon & Finnie %ENDCOMMENT%

Johnson, K.L., Contact Mechanics, Cambridge University Press, 1985

Johnson reviews Hertzian contact mechanics. For the case of two sphericial bodies pressed together the results are the same as Shigley (below) with a slightly more convenient notation:

[4.22] where F is the load, [p. 92] and [p. 92] , where the subscripts 1 and 2 refer to the spine tip and asperity radius of curvature, respectively.

The maximum pressure us at the center of the contact patch: [4.24].

The worst case tensile stress is at the periphery of the contact patch: [p. 94]. The actual failure will depend on the local stress state, number of cracks and fracture toughness of the material. However, it will be a function of the maximum tensile stress. Therefore we can write that . The quantity in square brackets is a constand depending on the materials, so that in the end, the maximum sustainable load is expect to vary as the square of the radii of curvature of the spine tip and asperity.

Sheldon, G.L. and Finnie, I., "The Mechanism of Material Removal in the Erosive Cutting of Brittle Materials," ASME Journal of Engineering for Industry, Nov. 1966, p. 393-400.

Sheldon and Finnie begin with the above Hertz contact models and proceed through a fracture analysis. They consider a small sphere impacting an elastic half space. They comment that initiation of cracking and failure follows a Weibull distribution and will depend on the fracture strength of the material below the contact and the local stress state. A somewhat complicated analysis follows, but the basic point is that failure will depend on the maximum tensile stress.

---

older stuff...

Shigley (see attached pages below) reviews the Hertz contact stress model for spherical and cylindrical contacts. For two spheres, the radius of the contact patch, a, is given by (Shigley [2-82]):

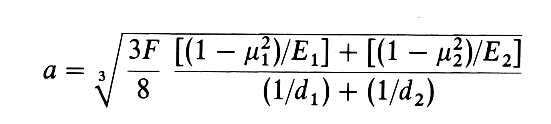
where F is the force, Ei are the elastic modulii of the two bodies and di are the radii of curvature of the two bodies. are the Poissons ratios for the two bodies.

Note that a is proportional to (Force x Length) to the one third power. The maximum pressure is at the center of the contact patch and is given by (Shigley [2-83])::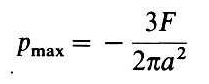
.
If we assume that failure occurs when some critical pressure is exceeded, we can combine equations 2-82 and 2-83 and solve for as a function of d:

Let and let

So 2-82 becomes . Then using 2-83 we have

or .

Going back to Momber and cementitious materials, Momber states in equation (7) that the maxium tensile stress is at the periphery of the contact patch: where the terms are the same as above from Shigley.

Chaining back to some older original sources... Iain Finnie (UCB?)

• An Experimental Study of Erosion, Proc. Soc. Exp. Stress Analysis, 17 (2), 65-70, 1960
• Erosion of Surfaces by Solid Particles, Wear, 3, 87-103, 1960.
• The Mechanism of Material Removal in the Erosive Cutting of Brittle Materials (with G. L. Sheldon), Trans. ASME, 88B, 393-400, 1966.
• An Analysis of Rock Drilling by Erosion (with H. Oh), Proceedings of the First Congress of the International Society of Rock Mechanics, 2, 99-104, 1966, published by Lab. Nacional de Engenharia Civil, Lisboa, Portugal.
• Flaws, Fracture Mechanisms and Hertzian Cracks in Brittle Solids (with D. Dolev), Proc. 4th Int. Conf. on Materials, 771-777, Stockholm, 1983.

-- MarkCutkosky - 09 Dec 2004