new web: http://bdml.stanford.edu/pmwiki
TWiki > Rise Web>ClimbingRobot > StickyBot>SolidMechanics (07 Jul 2006, AaronParness)
Rise Web>ClimbingRobot > StickyBot>SolidMechanics (07 Jul 2006, AaronParness)
-- AaronParness - 07 Jul 2006
My first thought was to do a wedge analysis with constant shear and normal stress along the bottom surface of the wedge:
 However, this formulation of the problem is likely incorrect. It is more probable that there is some sort of distribution along the bottom surface of the hairs that varies in location. To approximate what this varying shear load might be, I used the simple beam bending problem of a point force loaded on a beam built in at one end:
However, this formulation of the problem is likely incorrect. It is more probable that there is some sort of distribution along the bottom surface of the hairs that varies in location. To approximate what this varying shear load might be, I used the simple beam bending problem of a point force loaded on a beam built in at one end:
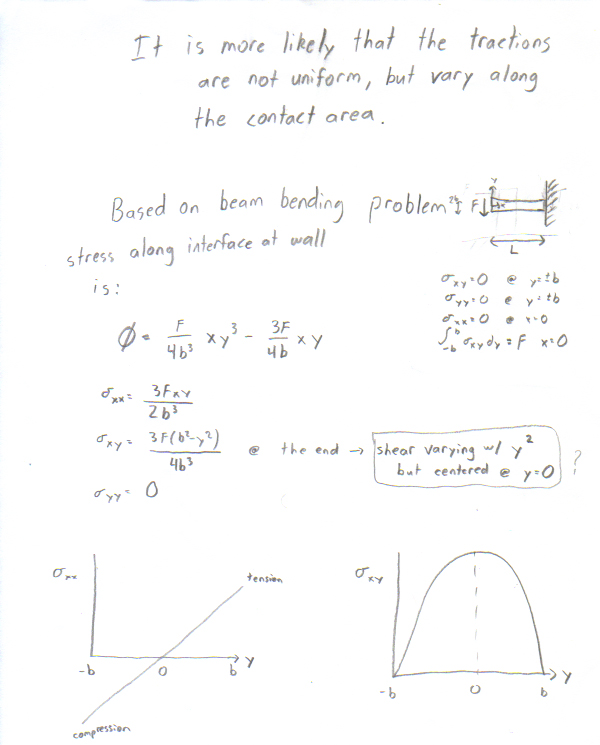 This yielded a shear force that varied as a quadratic, but the wedge problem is degenerate for n=-2 so I bumped up the distribution to a cubic variation in shear, but kept normal tractions constant along the bottom surface. Zero traction along the upper surface of the wedge:
This yielded a shear force that varied as a quadratic, but the wedge problem is degenerate for n=-2 so I bumped up the distribution to a cubic variation in shear, but kept normal tractions constant along the bottom surface. Zero traction along the upper surface of the wedge:
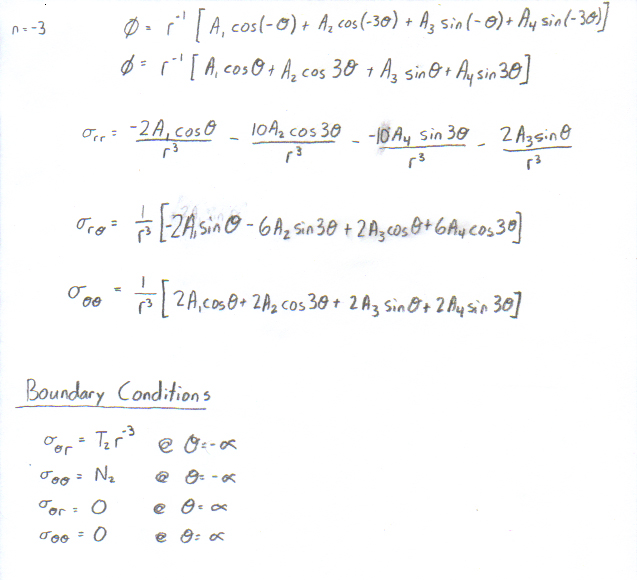
 This result is rather complex and it is difficult to base future designs on the dependencies of the stress on both the normal and shear multipliers. It is not transparent how the variation in angle 'a' might affect the stress in the body.
Next try will be an application of curved beam analysis to a built in end.
This result is rather complex and it is difficult to base future designs on the dependencies of the stress on both the normal and shear multipliers. It is not transparent how the variation in angle 'a' might affect the stress in the body.
Next try will be an application of curved beam analysis to a built in end.
 However, this formulation of the problem is likely incorrect. It is more probable that there is some sort of distribution along the bottom surface of the hairs that varies in location. To approximate what this varying shear load might be, I used the simple beam bending problem of a point force loaded on a beam built in at one end:
However, this formulation of the problem is likely incorrect. It is more probable that there is some sort of distribution along the bottom surface of the hairs that varies in location. To approximate what this varying shear load might be, I used the simple beam bending problem of a point force loaded on a beam built in at one end:
 This yielded a shear force that varied as a quadratic, but the wedge problem is degenerate for n=-2 so I bumped up the distribution to a cubic variation in shear, but kept normal tractions constant along the bottom surface. Zero traction along the upper surface of the wedge:
This yielded a shear force that varied as a quadratic, but the wedge problem is degenerate for n=-2 so I bumped up the distribution to a cubic variation in shear, but kept normal tractions constant along the bottom surface. Zero traction along the upper surface of the wedge:
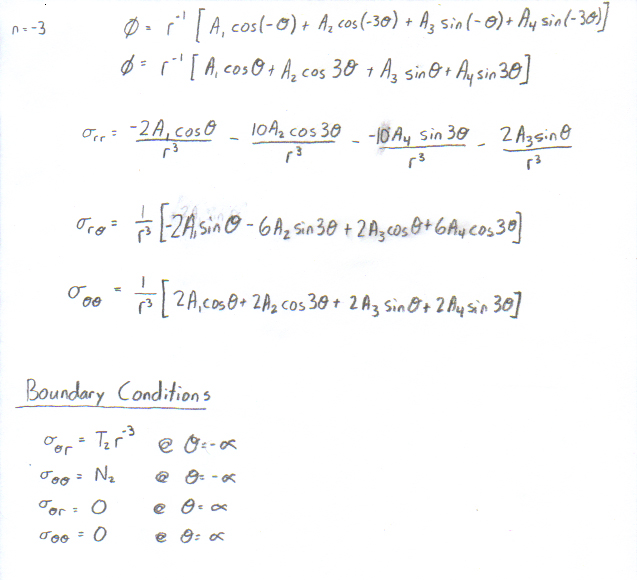
 This result is rather complex and it is difficult to base future designs on the dependencies of the stress on both the normal and shear multipliers. It is not transparent how the variation in angle 'a' might affect the stress in the body.
Next try will be an application of curved beam analysis to a built in end.
This result is rather complex and it is difficult to base future designs on the dependencies of the stress on both the normal and shear multipliers. It is not transparent how the variation in angle 'a' might affect the stress in the body.
Next try will be an application of curved beam analysis to a built in end.
Ideas, requests, problems regarding TWiki? Send feedback