new web: http://bdml.stanford.edu/pmwiki
TWiki > Manufacturing Web>ManufacturingHome > MaterialsInfo > UrethaneProperties>YoungsModuliForUrethanes (31 Jul 2010, DanAukes)
Manufacturing Web>ManufacturingHome > MaterialsInfo > UrethaneProperties>YoungsModuliForUrethanes (31 Jul 2010, DanAukes)
At Will's suggestion, I have computed the Young's modulus for the 20A polyurethane. If you do similar calculations in the future please put your results here.
-- AlanAsbeck - 27 Apr 2005
Contents of this page:
Testing the Maximum tensile strength of 20A:
Used a flexure 0.8 x 1.0 x 7.68 mm. It broke after about 60 grams. This gives us a maximum tensile strength of 108psi = 7.5e5 Pa.
Used 4 flexures in parallel of 0.8 x 1.5mm in cross-section. They broke after 400g. This gives a max. tensile strength of 181psi = 1.25e6 Pa.
A single flexure of 0.8 x 1.5mm in cross-section broke after ~115g ==> max tensile strength = 208 psi = 1.44e6 Pa.
BigToe.
Contents of this page:
Summary of Material properties:
| Material | Young's Modulus | Max. Tensile strength |
|---|---|---|
| IE-20A | 217 kPa | ~190 psi |
| IE-35A | 350 kPa | ~230 psi |
| Very old IE-50A | 200kPa | ? |
| IE-60A | 563 kPa | ~200 psi |
| Vytaflex 20A | 195 kPa | ? |
| Vytaflex 40A | 400 kpa | ? |
| Vytaflex 60A | 1.2-1.3 MPa | ? |
IE-20A:
Tested: a 20A flexure 7.76 x 0.78 x 1.49 mm. in F= k*x, k=32.46 N/m using the data between the 20g and 30g points (see figure below). l = .00776 m A = 1.1622e-6 m^2 E = k*l/A = 2.17e5 Pa = 217 kPa you can use the formula k=E*A/l to quickly compute how other flexure geometries will behave.
- 20A flexure used in testing:

- 20Astressstrain2.jpg:
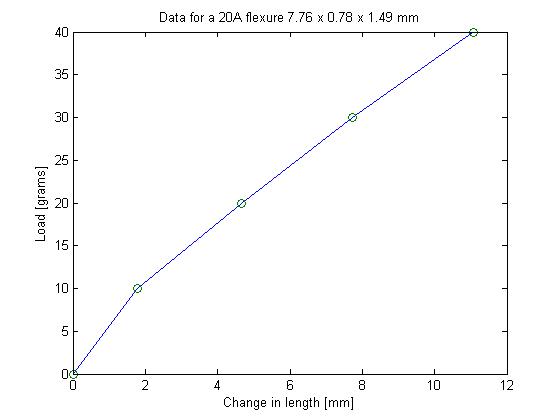
| Length [mm] | Change in length [mm] | Load [g] |
|---|---|---|
| 7.76 | 0 | 0 |
| 9.55 | 1.79 | 10 |
| 12.41 | 4.65 | 20 |
| 15.49 | 7.73 | 30 |
| 18.83 | 11.07 | 40 |
IE-35A:
Better measurements, using a new flexure of size 2.0 x 3.1 x 7.0 mm: Using the data points at 200g and 400g in the graph below (two flexures were measured), we computed E=350kPa. This is a reliable number. The flexures also broke at between 550-600g. Using the breakage data, we compute the Maximum Tensile strength to be 128 to 140 psi (= 8.9e5 to 9.7e5 Pa), much less than the 400psi stated on the Innovative Polymers website. We compute this by doing:Max_tensile_strength = Load_at_breakage[N] / Cross_sectional_area[m^2] to give the answer in N/m^2 = Pascals, then to convert to psi we do: psi = Pa * 1.4508e-4Using a different flexure of dimensions 2.0 x 1.86mm, which broke at 600g, we get 234psi = 1.6e6 Pa. I think this is an accurate number. HOWEVER, it is difficult to reach these limits because the 35A tends to develop stress concentrations at the interface to the 72DC, and break there at much lower loads.
- 35A:
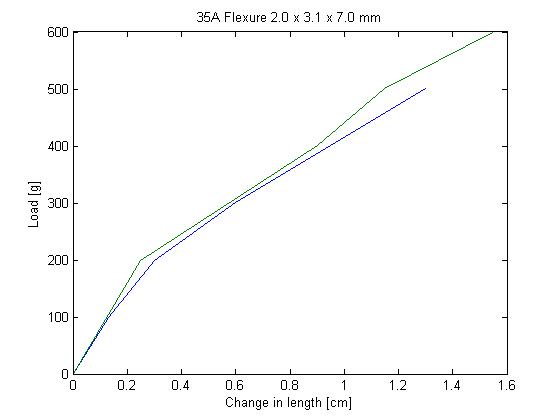
IE-60A:
Actual data: Flexture broke at about 1kg.| Length [mm] | Change in length [mm] | Load [g] |
|---|---|---|
| 54.01 | 0 | 0 |
| 60.62 | 6.61 | 100 |
| 68.5 | 14.49 | 200 |
| 81.3 | 27.29 | 300 |
| 97.08 | 43.07 | 400 |
| 114.08 | 60.07 | 500 |
| 128.27 | 74.26 | 600 |
| 139.33 | 85.32 | 700 |
| 149.02 | 95.01 | 800 |
- 60A Flexture Data:
Very old IE-50A:
The flexure measured was the main flexure from aWeight F x deltax k=F/dx [N/m] 0g 0N 4.86mm 0mm -- 100g 1N 8.53mm 3.67 272 200g 2N 16.4mm 11.54 173 300g 3N 25.5mm 20.64 145 400g 4N broke--delaminated after a little while deltax between 1N and 2N: 16.4-8.53=7.87 k = 1N/7.87mm = 127 ==> E = 127*4.86e-3/3.1e-6 = 200,000 = 200kPa dimensions 1.4mm thick 2.2mm tall (approximately) ==> A ~= 3.1 x 10^-6 E = k*l/A where l = original length
Vytaflex 20A:
| Weight | F | x | deltax | k=F/dx [N/m] |
|---|---|---|---|---|
| 0g | 0N | 2.34mm | 0mm | -- |
| 100g | 1N | 3.58mm | 1.24 | 806 |
| 200g | 2N | 5.29mm | 2.95 | 678 |
| 300g | 3N | 6.95mm | 4.61 | 651 |
| 400g | 4N | 9.2mm | 6.86 | 583 |
using k=650, E = 650 * 2.34e-3 / 7.83e-6 = 194,000 dimensions: 2.34mm long 1.45mm thick 3 x 0.8mm thick plus 3 x 1.0mm thick ==> Area = 1.45mm x (2.4mm + 3.0mm) = 7.83e-6
Vytaflex 40A:
| Length [mm] | Change in length [mm] | Load [g] |
|---|---|---|
| 13.5 | 0 | 0 |
| 15.9 | 2.4 | 100 |
| 18.7 | 5.2 | 200 |
| 22.24 | 8.9 | 300 |
| 28.2 | 14.7 | 400 |
| 32.1 | 18.6 | 500 |
| 39 | 25.5 | 600 |
| 44.5 | 31 | 700 |
| 52.1 | 38.6 | 800 |
| 57.4 | 43.9 | 900 |
- 40Aflexturedata.JPG:
- 40A:
Ideas, requests, problems regarding TWiki? Send feedback